Ali Kaya
“How can it be that mathematics, being after all a product of human thought which is independent of experience, is so admirably appropriate to the objects of reality?”
Albert Einstein
I have always been pretty sure that mathematics and science are the best languages to explain the natural phenomena. While for many mathematics is too abstract, for me, it is the beautiful language of the universe.
There is no upper limit to the numerical abilities of humans. First, we discovered fire, to get warm. Then, we needed light, so we invented electricity. When we needed to talk to someone 10,000 miles away, we invented the internet. Behind all these inventions, was mathematics.
Of course, the universe cannot speak or think. However, we, the people, can read the universe. There are many scientifically and mathematically inclined people who can read the universe and find answers and then describe them. We, the normal people, can also use our imagination as an apparatus to read the universe and nature. If we can read, hence, something is written. In order to write, a language is always needed. So, the universe should have a language. The letters are circles, triangles, hexagons, etc.
Everything in life has mathematical patterns. Think of the wild animals with stripes or patterns for the purposes of camouflage. But why does a leopard or cheetah or tiger have a particular design?
The Enigma codebreaker, Alan Turing, had a mathematical theory about leopard’s spots. Turing suggested in his paper “The Chemical Basis of Morphogenesis” (published in 1952) “a mathematical schema for the formation of the patterns found in animals and plants.” This was 60 years ago [1].
Stars have patterns. Astrologists have been looking at the outer space searching for patterns to better understand life. Whatever it may be that they find, it is always about mathematics.
Seasons have patterns. They come and go. And they influence nature: the climate changes, animals migrate north or south, rain comes, snow melts, the earth changes color, etc.… Of course, seasons cannot make these miracles. They can only have mathematical patterns.
Einstein had pondered for years on how mathematics works so perfectly. He knew that mathematics is the bridge or the language that connects humans with the universe. And being a connection between us and the universe makes mathematics the greatest achievement of mankind.
If you take a closer look at the patterns of our world, you will witness the language of mathematics. Let me give you some specific examples.
Fibonacci, the golden ratio, spiral, cabbage…
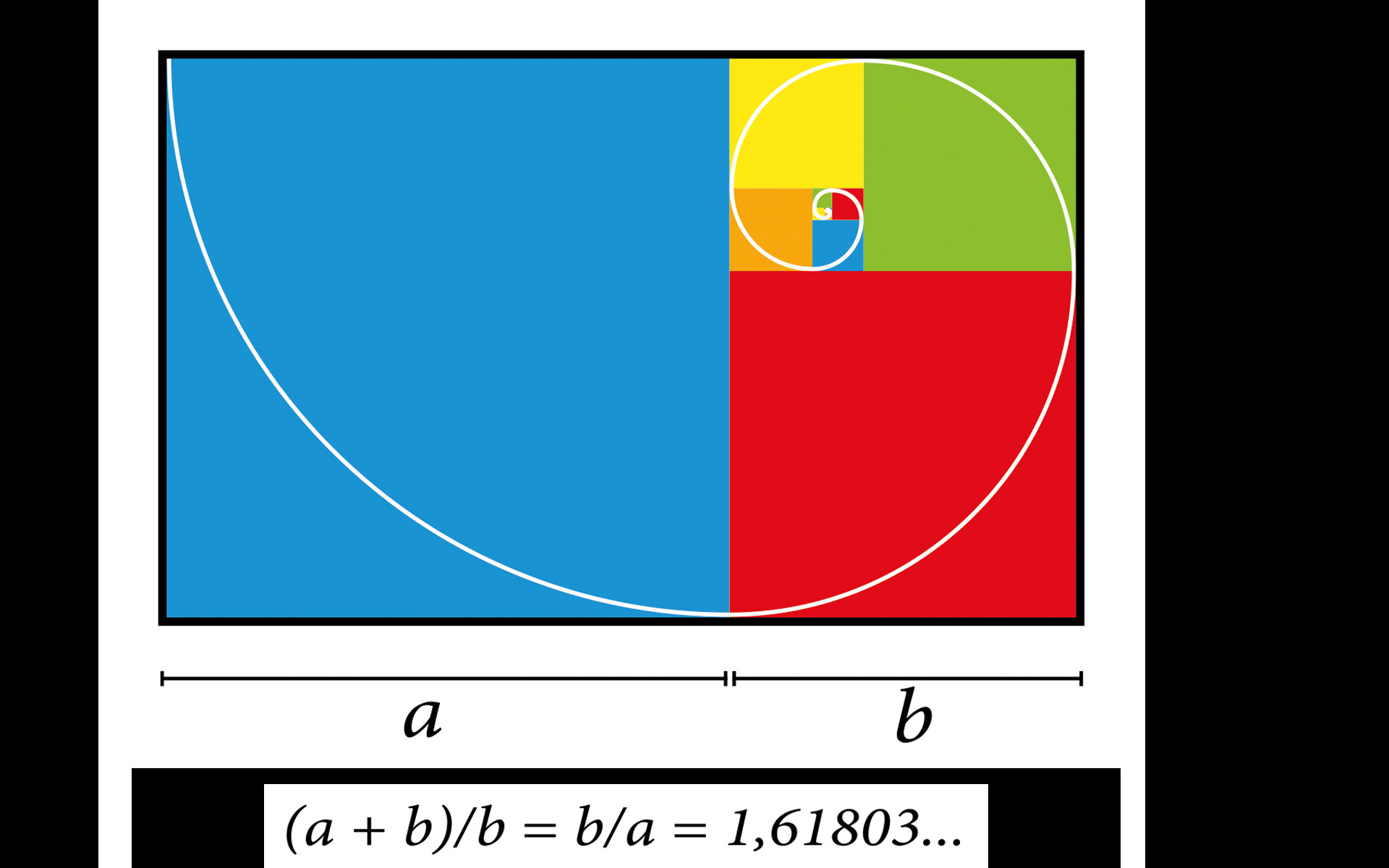
Our universe is filled with spiral designs. Spirals can be found in the shapes of the DNA double helix, flowers, elephant tusks, sunflowers, hurricanes, draining water, animal horns, a nautilus shell, a snail shell, a pinecone, a cabbage, a fingerprint, algae, galaxies... the list goes on and on. Tons of lifeless and living things have spiral designs. And they are not random spirals. They have something in common: the golden ratio! And surprisingly, “there is a strong case that this so-called ‘Golden Ratio’ (1.61803...) can be related not only to aspects of mathematics but also to physics, chemistry, biology and the topology of space-time” [2].
 |
 |
 |
All these spirals in nature tell us there are numbers all around us. Let’s observe the numbers of petals on some flowers. When you count the number of petals of the flowers in your garden, you will get the numbers 3, 5, 8, 13, 21, 34, or 55. These numbers are not random numbers. These are very unique numbers; they are part of a sequence developed by Fibonacci, a 13th century mathematician, by adding up the last two numbers starting from 1:
1+1= 2, 1+2= 3, 2+3= 5, 3+5=8 …
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Fn= Fn-1+Fn-2, F1=1, F2=1
But, why are those Fibonacci numbers so important? The key is, the relationship between the progression of growth and the proportion. There is a harmonic proportion hidden in the Fibonacci sequence.
A fact: If you divide one number in the sequence by the previous number, the answers result in or come closer to phi:
For example: 5/3 = 1.6666;
13/8 = 1.6250; 377/233 = 1.61802575; 317811/196418 = 1.618033399
Definition: In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities [3].

These numbers can be demonstrated with the spiral of the florets in a sunflower. The florets in a sunflower head also form two spirals. If you count the clockwise and counterclockwise spirals that reach the outer edge, you’ll usually find a pair of numbers from the sequence: 34 and 55. If it is a very large sunflower, you will get 89 and 144 [4].
These spirals are not only in sunflowers. You can see them if you look at a pine cone or a daisy. If you mark the spirals and count them, you will always get a number from the Fibonacci sequence. And if you count in the other direction, this time you will find an adjacent Fibonacci number.
The nautilus shell, the golden mean
What makes the nautilus shell so special for mathematicians? Having the Golden Mean. But how do we know that the nautilus shell has the Golden Mean?
First of all, we will start with drawing a small, one unit square. Then we will draw another square which is larger than the previous one. We need to add in a counterclockwise direction. The length of each square has a value from the Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 … Then we can draw spirals, starting with the smallest one, outward through the largest one. Then the Golden Mean will appear.
Flowers, plants, or objects have no idea about mathematics, yet they manifest the best of mathematical patterns. This marvelous mathematical art has been placed in their nature for us not to be fascinated only but also to explore the mysteries behind it.