Fatih Gelgi

Figure 1: Drawing hands, 1948
Maurits Cornelis Escher (1898–1972) is one of the world’s most famous graphic artists of impossible structures (e.g. “Ascending and Descending”) and transformation prints (e.g. “Metamorphosis I-II-III”). Currently, one can see his work on posters, book covers, calendars, wall hangings, and many web sites enjoyed by millions of people all over the world (1).
His exquisite and mind boggling pictures are drawn from the mathematical world of symmetry, topology, transformational geometry, and regular divisions of the plane. At the same time, they exhibit a rich and artistic talent unrivaled by most. Furthermore, respected scientists have realized that his works are simple illustrations of sophisticated theories (2). For instance, mathematician D.J. Lewis indicates that Escher’s prints entail a systematic approach combined with an ingenious argument similar to the most beautiful results in algebra. In 1952, Herman Weyl, a Princeton mathematician, used Escher’s famous work “Symmetry” for his book cover. Escher’s rendering of “Horseman” was used by Chen Ning Yang, a physicist and Nobel Prize winner, to illustrate his new hypothesis involving symmetry and its application to quantum physics (3). Escher has also inspired scientists in their academic studies. For example, some of his sketches helped his half-brother B.G. Escher, a professor of geology, in solving crystallography problems (4).
Tessellation of a plane, also called tiling, is the mosaic formed by filling the plane with no gaps and no overlaps. A person who is familiar with Islamic art immediately notices the deep connection between Escher’s transformational geometry and tessellations, and that of Islamic patterns. One can even use Islamic art and tessellation techniques to generate Escher-like drawings. In fact, Escher’s 1922 visit to the Alhambra Palace in Spain was the turning point in his life. He was fascinated and inspired by the spiritual significance of the tile work at the palace, and Islamic patterns played a key role in transforming his art (5). This article will explore the intimate relationship between Islamic art and Escher’s work, in particular the significance of themes with “flat surfaces” and “flat surfaces with respect to pictorial representations.”
Brief summary of Escher's art
Escher produced 448 lithographs, woodcuts, and wood engravings and over 2000 drawings and sketches during his lifetime (1). His understanding of mathematics was largely visual and intuitive, and his works display a strong mathematical component (6). More than 150 of colorful works testify to his ingenuity in regular division of plane. He was very successful at depicting the real world in 2-dimensional plane as well as at translating the principles of regular division onto a number of 3-dimensional objects such as spheres, columns, and cubes. Some of his prints combine both 2 and 3-dimensional images with a startling effect as demonstrated in “Reptiles” (7).

Figure 2: Reptiles, 1943
Upon further examination, one finds three dominating themes in Escher’s works (2):

Figure 3: Atrani, Coast of Amalfi, 1931

Figure 4: Day and Night, 1938
• Flat surfaces with respect to pictorial representation: Escher’s final and most famous type of work is his portrayal of “impossible structures.” He was very skilled at illustrating three-dimensional conflicting situations in two-dimensional spatial representations (8).
Figure 5: Waterfall, 1961

Patterns in Islamic art
In Islamic art, the spiritual world is regarded as being reflected in nature through geometry and rhythm. Hence, Islamic artists used geometry as an aid to raise their spiritual understanding as well as the viewer’s:
“Muslim intellectuals recognized in geometry the unifying intermediary between the material and the spiritual world. These patterns may be seen as symbolizing the Islamic principles of ‘Tawhid’ (the unity of all things) and ‘Mizan’ (order and balance), which are the laws of creation in Islam.”(9)
Tessellations are one of the major components of Islamic art. Islamic artists mastered regular division of plane using, in particular, circles on triangular or square grids, because the circle – which has no beginning and no end and thus symbolizes infinity – was considered to be the most perfect geometric form. In mosques, where a wealth of these geometric patterns could be found, one could contemplate the infinite nature of God simply by looking at the walls or ceiling. In short, these geometric forms expressed Islamic artists’ fascination with mathematics as a metaphor for divine order and presence (10). Figure 6, Figure 7, Figure 8, and Figure 9 are examples of triangle and square grids and produced patterns adopted from (11):

Figure 6: Triangular grid (a) and examples of patterns: (b) 6-pointed star-hexagon (c) Ceramic wall panel - Iran - 13-14th centuries.
Figure 6 demonstrates the 6-pointed star-hexagon pattern that can be obtained by coloring a triangular grid whereas Figure 7 integrates circles to produce more complicated patterns and an increase in variety. The examples shown in the figures are real tiles mounted in mosques around the world.

Figure 7: Triangular grid and examples of patterns.
Figure 8 and Figure 9 illustrate the usage of circles on a square grid in two different ways. The square-hexagon pattern in Figure 8(c) is commonly used on the ceilings of mosques whereas variations of the star-cross pattern in Figure 8(c) have mostly been used on walls.
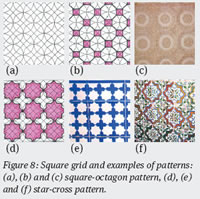
Figure 8: Square grid and examples of patterns: (a), (b) and (c) square-octagon pattern, (d), (e) and (f) star-cross pattern.
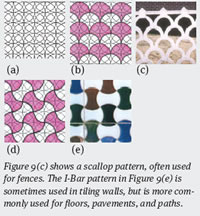
Figure 9(c) shows a scallop pattern, often used for fences. The I-Bar pattern in Figure 9(e) is sometimes used in tiling walls, but is more commonly used for floors, pavements, and paths.
Figure 9: Square grid (a) and examples of patterns: (b) and (c) scallop pattern, (d) and (e) I-bar pattern.
The Alhambra’s influence on Escher

Figure 10: (a) A view of the Alhambra, (b) the Lion’s Court in the Alhambra, which inspired Escher’s drawing.
Escher became fascinated by the regular division of the plane in 1922 when he first visited the Alhambra, a fourteenth-century Moorish castle in Granada, Spain. (1). He then studied Polya's seventeen plane symmetry groups, (thirteen of which are displayed in the Alhambra), and Haag's mathematical definition of the division of the regular plane (12). But the real metamorphosis in his art began in 1936, with his second visit to Alhambra, which he described as “the richest source of inspiration” in his writings (5). Like many Islamic artists, Escher believed that repetitive patterns indicated a higher source of knowledge that existed before mankind. He considered order, regularity, cyclical repetitions, and renewals to be the “laws of the phenomena” around us; accordingly, the structure of his designs was a simple reflection of these laws from his own perspective (9).
Escher studied, took detailed notes, and made sketches of the tile patterns at the Alhambra. In his writings, he described his fascination with the double use of contours and divisions of the plane as follows:
“The Moors were masters in the filling of surface with congruent figures and left no gaps. In the Alhambra, in Spain, especially, they decorated the walls by placing congruent multicolored pieces of majolica together without interstices.”(8)

Figure 11: Examples of patterns in the Alhambra (adapted from http://www2.spsu.edu/math/tile/grammar/moor.htm)
In his later work, Escher used genuine techniques devised from triangular and square grids, applying reflections, translations, and rotations to obtain great variety of patterns in his tessellations. The simple trick of modifying the grids utilized in Islamic art to ensure the perfect fit of patterns, which Escher used in his tessellations, is demonstrated below:
Figure 12: An example of an Escher-like pattern obtained from the rectangle (adopted from (11).
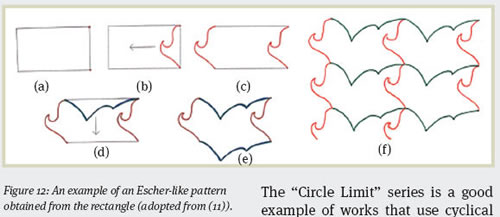
The idea is to start with a pattern such as a rectangle in Figure 12(a). The tessellation pattern is created by cutting portions of the pattern as in Figure 12 (b) and (d), and mounting them to the correct locations of the pattern considering the rotations and reflections as in Figure 12 (c) and (e). Finally, the pattern is rendered in tile as illustrated in Figure 12(f). One can imagine how easy this novel technique was to apply, yet how complicated it was to discover.

Figure 13: Escher's symmetry drawings produced from (a) diamond, (b) rectangular, and (c) I-bar patterns. The grids are placed on the original images to reveal the relationships.
Figure 13 presents examples of Escher’s symmetry drawings. Figure 13(a) utilizes a diamond pattern by converting it to a man applying a rotation of 120. whereas Figure 13(b) was created from a rectangle with a rotation of 180. In Figure 13(c), Escher was able to take the I-Bar pattern and adapt it to the totally dissimilar motifs of angels and devils.
In many of Escher’s tessellations, not only the patterns, but also the entire scene is inspired by the circle and eternity as in Islamic art. The “Circle Limit” series is a good example of works that use cyclical tiling with shrinking patterns from the center to the border in a circle. Although a circle is depicted, the patterns theoretically reach an infinitive number of repetitions on the border. In his “Metamorphosis II,” it is also interesting to see that a closed cycle is formed when the two vertical ends of the picture are joined together. Similarly, in his famous woodcut ‘Day and Night,’ which shows black and white birds flying in opposite directions, not only do the birds and landscape complete cycles, but also the print is symmetric with respect to a vertical line (4).

Figure 14: Convex and Concave, 1955
Another famous work by Escher, “Convex and Concave,” exemplifies his “impossible reality” works. The essential idea that governs the entire lithograph is the Islamic tumbling baby block pattern, which appears in the flag on the upper right side. Although the picture, as a whole, seems to portray a normal scene, it actually consists of multi-purpose planar surfaces. Depending on the location upon which the eye focuses, the same planes may serve as ceilings, walls, or floors. Escher’s “Waterfall,” “Ascending and Descending,” “Relativity,” and “House of Stairs” all present similar mind-boggling characteristics (2).
In conclusion, Escher is a world-famous graphic artist, well-known for his impossible structures and transformation prints. He is one of the unique figures appreciated for his ability to apply his mathematical talent in artistic creation. He was strongly influenced by the Islamic patterns in the Alhambra – a fourteenth century palace in Spain. He developed his extraordinary style and mastered his skills after exploring the tessellation techniques Islamic artists used to create the figures in the Alhambra.
Fatih Gelgi has a PhD in computer science. He is currently the computer coordinator of Accord AMSP team in Los Angeles.
Bibliography
1. M.C. Escher, the Official Website. [Online] [Cited: January 10, 2009.] http://www.mcescher.com/.
2. Desoe, Carol D. Marthematics: The Blending of Mathematics and the Art of M.C. Escher. [Online] [Cited: December 10, 2008.] http://caroldesoe.com/IslamicArt/mARThematics.pdf.
3. Broos, C.H.A. Escher: Science and Fiction. In: J.L. Locher. The World of M.C. Escher. New York : Abradale Press, 1988.
4. Locher, G.W. The Work of M.C. Escher. In: J.L. Locher. The World of M.C. Escher. New York : Abradale Press, 1988.
5. Abbas, Jan S. Islamic Patterns: The Spark in Escher's Genius. In: Doris Schattschneider, Maurits Cornelis Escher and Michele Emmer. M.C. Escher's Legacy. New York : Springer, 2005.
6. M.C. Escher. Wikipedia. [Online] [Cited: January 10, 2009.] http://en.wikipedia.org/wiki/M.C._Escher.
7. O'Connor, J.J. and Robertson, E.F. Maurits Cornelius Escher. School of Mathematics and Statistics. [Online] May 2000. [Cited: December 21, 2008.] http://www-history.mcs.st-andrews.ac.uk/Biographies/Escher.html.
8. Ernst, Bruno. The Magic Mirror of M.C. Escher. New York : Barns & Noble Inc., 1994.
9. Islamic Patterns and M.C. Escher's Tessellations. North Texas Institute for Educators on the Visual Arts. [Online] [Cited: December 6, 2008.] http://www.art.unt.edu/ntieva/pages/about/newsletters/vol_14/no_1/.
10. Melikian-Chirvani, A. S. Treasure of Islam. New Jersey : Wellfleet Press, 1985.
11. Islamic Art through the Eyes of M. C. Escher. Desoe, Carol D. Salt Lake City : NCTM Annual Meeting, 2008.
12. Schattschneider, Doris. Visions of Symmetry: Notebooks, Periodic Drawings, and Related Work of M.C. Escher. New York : W.H. Freeman and Company, 1990.
13. Graber, Oleg. Arts of Islamic Peoples. Encyclopedia Britannica. 1974, Vol. 9.









