Ihsan Kose
Scaling in biology explains how a system?s characteristic is affected when another dependent factor changes. One of the prime examples of scaling has to do with metabolism. The average energy spent by a resting organism (the basal metabolic speed) is strongly related to the organism?s body mass, and this points to the presence of a scaling mechanism. The conversion of food, water, air, and light into usable energy is a major process for all organisms: it is necessary for metabolism and contains vital information on how life is maintained.
It has been well known for a long time that the metabolisms of smaller animals are faster when compared to the metabolisms of larger animals relative to their body size. In 1883, German physiologist Max Rubner tried to define a scaling principle based on the laws of thermodynamics and geometry. The metabolism of an organism works like a perfect machine that continuously converts one form of energy into others. It also releases energy while doing so. Metabolic speed can be described as the speed at which cells convert nutrients into energy. This energy is utilized for the execution of cellular functions and the construction of new cells.
Calculations have shown that the speed of metabolism is directly proportionate to body mass. For instance, the biomass of a hamster is eight times bigger than a mouse. According to this ratio, one would expect the metabolism of a hamster to be eight times faster than that of a mouse. Similarly, the body mass of a hippopotamus is 125,000 times larger than a mouse; therefore its metabolism would be estimated to be 125,000 times faster.
The problem is that a hamster generates eight times more heat than a mouse. Furthermore, the total body surface area, which is how the heat energy leaves the hamster?s body, is four times bigger than the surface area a mouse has. Consequently, as the body of an organism grows, its surface area develops more slowly compared to its mass.
This situation is shown in Figure 1. Here a mouse, a hamster, and a hippopotamus are represented in spheres. As the spheres get larger, their volume and surface area also gets bigger. In geometry we know that the volume of a sphere is given as? ![]() ?(r is the radius of the sphere). The surface area of a sphere is also expressed as
?(r is the radius of the sphere). The surface area of a sphere is also expressed as ![]() . In this case we can say that while the volume of a sphere is scaled with the cubed radius, the surface area of a sphere is scaled with the squared radius. In other terms, the volume of a sphere is directly proportionate to the cubed radius, as is the surface area of the sphere to the squared radius.
. In this case we can say that while the volume of a sphere is scaled with the cubed radius, the surface area of a sphere is scaled with the squared radius. In other terms, the volume of a sphere is directly proportionate to the cubed radius, as is the surface area of the sphere to the squared radius.

Figure 1. The scaled features of a mouse, hamster, and hippopotamus. Taken from Complexity: A Guided Tour by Melanie Mitchell, Oxford University Press.
Figure 1 displays the first model used by scientists when the relation between metabolic speed, body mass, and surface area was being investigated. According to this early model, the association between body mass, surface area, and volume was studied with spheres that encased organisms. As the volume of the sphere approximately provided the volume of the organism, the sphere?s surface area also represented the surface area of the organism (of their skin). According to this, the radius of the sphere containing the hamster is nearly twice as large as the radius of the sphere with the mouse. Therefore, it can be claimed that the volume of a hamster is approximately eight times the volume of a mouse, and its surface area is four times larger. When it comes to the hippopotamus; the radius of the sphere is 50 times larger than the one with the mouse; this shows it has a 2500 times wider surface area and a 125,000 times larger volume compared to the mouse.
As it can be seen with these examples, while the radius of the sphere increases, its surface area does, too, but at a slower ratio compared to the volume ? in other terms, it gets scaled.
Based on this model, since the surface area is scaled (enlarged) with the square of the radius, and the volume with the cube of the radius, it can be estimated that the surface area is scaled with 2/3 the power of the volume.
The interesting point that all these rough calculations take us to is that the surface-area width of the living things is adjusted in a way to permit the release of energy they generate into their surroundings in a healthy pattern. If a hamster generated more heat than the amount corresponding to four times its surface area, this would lead to the hamster overheating.
In a similar way, if you elevated the heat in a hippopotamus, which generates 125,000 times more heat than a mouse does, by eight, the hippopotamus would suffer from heat exhaustion. This is because the surface area of a hippopotamus is only 2500 times bigger than a mouse. This is called the ?surface hypothesis,? and until it was discovered that it does not correlate well with the experimental data, scientists carried out investigations based on this model for nearly 50 years.
Around 1930, Swiss animal scientist Max Kleiber performed a series of studies involving the metabolic speed of various animals. The data he collected showed that the metabolic speed is scaled to ? the power of body mass, or Metabolic speed = body mass3/4.? This is called the power law in science. Instead of the 2/3 power in the first model, the correlation of 3/4 power with the experiments demonstrated that animals, especially large ones, have higher metabolic speeds than the first model predicted.
In summary, the establishment and maintenance of this equilibrium requires knowledge beyond geometric calculations, and makes it impossible to explain via random occurrences.?
In Figure 2, the scaling of different animals in regard to their body mass is charted. The horizontal axis shows the body mass in kilograms, whereas the vertical axis marks the speed of their average basal metabolism in watts. The symbols displayed as dots are real values measured from different animals and the fact that these dots align almost on a line show the correlation of the metabolic speeds of organisms with 3/4 the power of their body masses. This points to an extraordinary order in the universe, one that has been created with perfect harmony built into it. ?
One feature of the ?power law? is that when the two axes are drawn logarithmically, the relation between the two physical magnitudes appears as a line. Here, a similar situation is present and this power law is called the ?Kleiber Law.? This law successfully provides the metabolic speeds of mammals, birds, fish, plants, and even single celled organisms.
There are also other scaling relations pertaining to these that have confounded biologists for a long time. For example, the bigger a mammal is, the longer its life span is. There are examples, like humans, who do not fit into this general principle. However this is applicable for many mammals. The life of a mouse lasts two years, typically, whereas the life of a pig is around 10 years ? and elephants live for 50 years. If you chart the average life span of many different species across their body masses, the value of the power law is seen as ?. In other terms, for mammals, the average life span is scaled to ? of the body mass (directly proportioned).
As another example of proportion and scale, if you draw a graphic displaying how the average heart beat speed changes against the body mass of different species, you will once again find the scale of the power law to be ?. This means that the larger the body mass of a mammal, the lower its heart beat is.
Biologists are trying to solve the mysteries among the relations of many power laws like this one. There is no doubt among scientists regarding the fact that these power laws manifest certain common features in living things as an important sign pointing to the presence of very significant common features for all organisms.
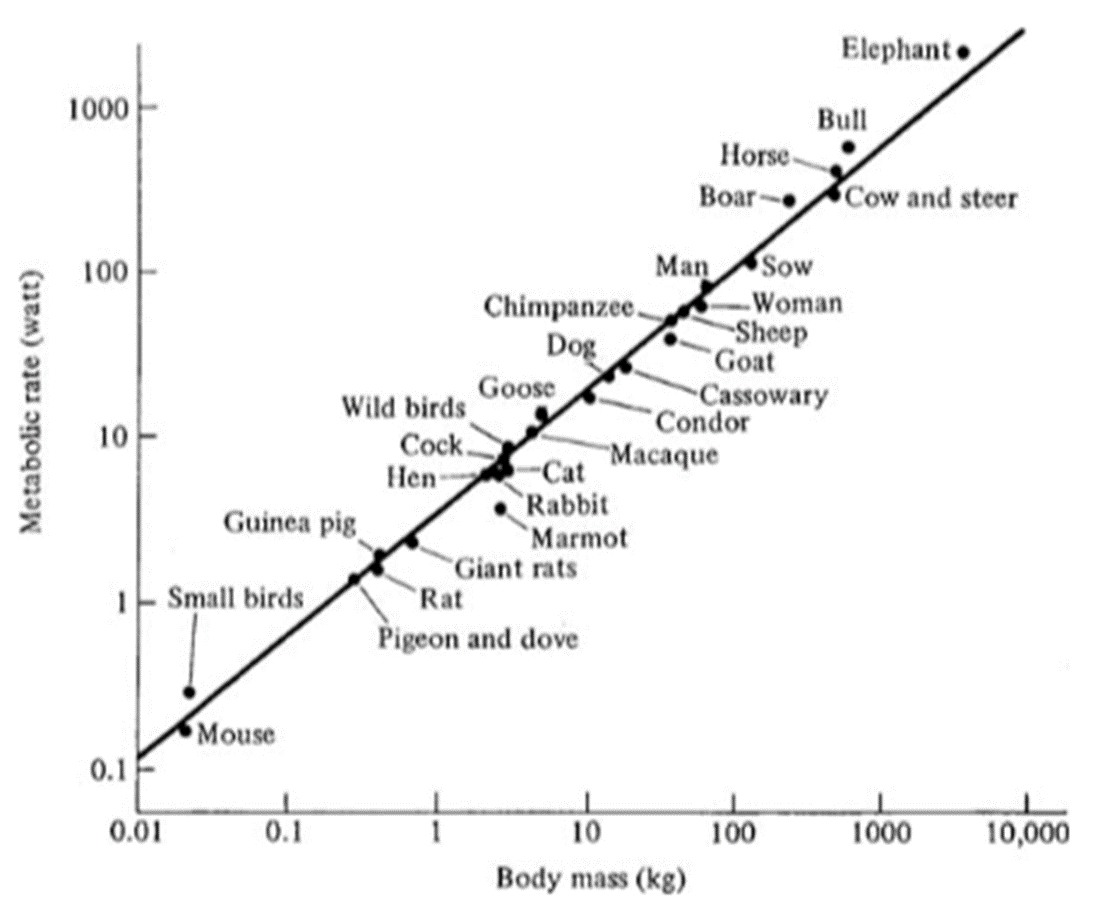
Figure 2. Metabolic speeds of different animals according to their body masses. Taken from Complexity: A Guided Tour by Melanie Mitchell, Oxford University Press.
The creation of living things according to a power law, which is a relation between their metabolic speeds and body sizes, is a wisdom that requires thanksgiving. To safely release their generated energy, the metabolic speeds of living things must be scaled to ? the power of their body mass. A lower value would cause a higher body heat, and a higher value would lead to very low body heat. In both situations it would not be possible for organisms to sustain their lives in the physical world. Our bodies are perfectly scaled for us to survive.
Note
Experimental values were obtained from the book of - K. Schmidt-Nielsen, Scaling: Why is animal size so important?, Cambridge University Press, 1984.
Reference
- Complexity - A Guided Tour, Melanie Mitchell, Oxford University Press, 2009.









